Comonads

Preview

Monads are popular, but not special. We show a number of examples where comonads can be used to solve interesting problems. The talk is meant to be a nice introduction into comonads, trying to glimpse at the theoretical basis while giving practical examples.

Summary

In functional programming, constructions using monads are common and even popular, even though they aren’t special in any regard; they were simply discovered and connected to their useful counterparts sooner than other category-theory related structures. To show why comonads should be studied and for what they can be used, we start with a short introduction of the important category theory terminology that will be used throughout the presentation.

Category theory redux

A collection (a term deliberately devoid of formal meaning) C of objects connected by arrows is called a category. The only two important rules a category has to satisfy are:

1. Every object X has an identity arrow idX = X → X
2. For two arrows, f = X → Y and g = Y → Z, there exists an arrow called a composition f ∘ g = X → Z.

Outside of the existence of identity arrows, objects in a category have no other properties, nor content. They are simply names; placeholders for identity arrows.

Arrows (formally called morphisms, meaning “shape preserving”), on the other hand, are defined by their source and target. The existence and collection of arrows defines what a category represents.

If one imagines a category, what one is imagining is basically a directed graph: the graphical interpretation of objects as points and morphisms as arrows. Now if one was to imagine two categories one next to the other, one could imagine that they are zoomed out enough to be just points. They could almost look like objects in some higher category (one where categories were objects and mappings between categories were morphisms). Any such mappings that also preserve the internal structure of the two categories, as described below, are called functors.

Any functor F = C → D must satisfy the following:

1. For any object X in C, F(X) maps to an object Y in D.
2. For any morphism f = X₁ → X₂ in C, F(f) maps to a morphism g = F(X₁) → F(X₂) in D.

An important thing to note is that there is a universal operation that can be done to anything that consists of points and arrows: one can flip all the arrows they see. This is the process through which we reach a structure’s dual. Duals to structures usually get the prefix “co-”. This is an important detail because we will be talking about comonads.

Functorial structures

Many functorial structures have found their way to widespread use in computer science. Potentially the one widest spread is the functor, which only describes a transformation which preserves structure, with the following signature:

(A => B) => (F[A] => F[B])

For the uninitiated, this can be read as “if you give me a way to transform an A into a B, I can give you a way to transform a structure over A to a structure over B.”

Many other similar useful transformations exist, including contravariant functors (which we discussed behave like sinks), applicative functors (which enable us to lift (apply) functions directly to functors), monads and comonads. The last two are the topic of our conversation, and their chaining operations have the following signature:

// monadic bind (>>=)
(A => F[B]) => (F[A] => F[B])

// comonadic extend, cobind (=>>)
(F[A] => B) => (F[A] => F[B])

The first one says that if we can find a way to create a monadic context (add a computational side-effect F to a transformation from A to B), then we can turn any side-effectual F[A] into an F[B] by chaining said computations. Its dual suggests a similar, yet opposite construction: if we can get some value B from an already wrapped F[A], then we can construct a wrapped F[B] from any F[A]. Where the monad is chaining computational effects as a post-condition, the monad requires the computational effect as a pre-condition for the function to happen, in a way.

There’s some shifty explaining here that uses the words (produce and consume), which doesn’t sit well with everyone, depending on context.

Examples

We show some uses for comonads on the deliberately overlapping examples of annotated structures, pointed structures and signal/stream processing (mostly used in functional reactive programming).

The following images are useful when trying to imagine what happens to any comonadic data structure when duplicated (this isn’t a tree, but close enough): .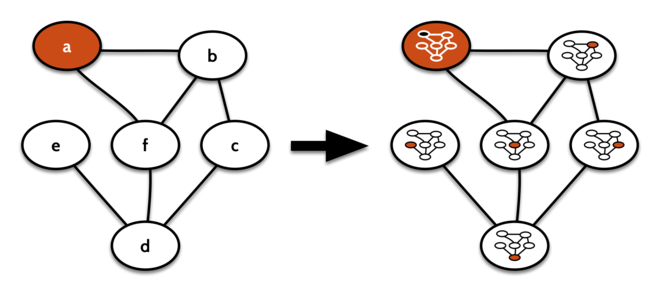

The second example shows how one can use comonads to implement pipeline structures which care only about locality (cellular automata, image pipelines, shaders, parallel programs, etc.), using the concept of the comonad having a pointed structure: focusing on a single element while allowing it to see its immediate environment.

The last example is only skimmed over, as everything shown previously all of a sudden falls into a familiar place: streams, zippers, etc. and the focused nature of computation is familiar to us from signal processing and functional reactive programming, where every variable is a stream of values in exactly this way. There’s several interesting connections to modelling OO programming and lenses, stores and states, which are mentioned in passing.

Getting comonads from arbitrary functors

Two ways in which one can extract a comonad from a functor is by applying the Cofree comonad to it, or by finding a functor pair that form adjoints. The Cofree comonad is a way to describe the computation of any comonad given only a starting element and a functorial structure, but this method is much less useful in the field, as it is mostly not interesting. It does, however, form a valid basis for comonadic constructions.

The adjoint pair extraction process is not shown in the slides and is given here in full:

trait Adjunction[F[_], G[_]] {
  def left[A,B](f: F[A] => B): A => G[B]
  def right[A,B](f: A => G[B]): F[A] => B
}

As an example, one example of an adjoint might be given as:

def adj[R] = new Adjunction {
  def left[A,B](f: ((A, R)) => B) =
    Function.untupled(f).curried

  def right[A,B](f: A => R => B) =
    Function.uncurried(f).tupled
}

The left adjoint generally adds structure, while the right one removes it, and thus the hazy notation from before returns: the left produces structure, while the right forgets it. The haziness might come from the fact that I said (and read) “produces/consumes values”, while we’re actually talking of structure.

For any such adjoint as defined above, the following two functions do magic:

def monad[F[_],G[_]](A: Adjunction[F,G])(implicit G: Functor[G]) =
  new Monad[λ[α => G[F[α]]]] {
    def unit[A](a: => A): G[F[A]] =
      A.left(identity[F[A]])(a)

    def bind[A,B](a: G[F[A]])(f: A => G[F[B]]): G[F[B]] =
      G.map(a)(A.right(f))
  }

def comonad[F[_],G[_]](A: Adjunction[F,G])(implicit F: Functor[F]) =
  new Comonad[λ[α => F[G[α]]]] {
    def counit[A](a: F[G[A]]): A =
      A.right(identity[G[A]])(a)

    def extend[A,B](a: F[G[A]])(f: F[G[A]] => B): F[G[B]] =
      F.map(a)(A.left(f))
  }

By applying it to the adjunction defined above, we can see that:

:t monad(adj[S]) 
// [S] => Monad[[α]S => (α, S)] = State[S, ?] monad

:t comonad(adj[S])
// [S] => Comonad[[α](S => α, S)] = Store[S, ?] comonad

This method, even though utterly brilliant, still isn’t really useful on its own, as it’s usually a bit faster and more readable and useful to just write the (co)monads by hand than to derive them this way.

References

The presentation was a shameless rip of this brilliant one. I was greatly helped in understanding the parts that were murky by A Scala Comonad Tutorial, Part 1 and A Scala Comonad Tutorial, Part 2. The pretty graph above is from here!

As I feared, the further into category theory I go, the less helpful Bartosz Milewski is, and this was true here as well. I’ve tried reading this, but it’s not particularly helpful or just not to my taste anymore. Feel free to give it a try anyway.

The haskell Control.Comonad library documentation is really good. Not really at my noob level, but the other resources help with that. The pointer example was reworked from A Comonadic Array. I watched hours of these people arguing politely and they were very good at showing some next-level functional understanding. I hope to be like them one day. That hat. The mentioned effect/coeffect system is from Tomas Petricek.

Tarmo Uustalu is a very common (no pun intended) name in comonadic circles. Examples include The Essence of Dataflow Programming, Recursion Schemes from Comonads and When is a Container a Comonad?. The answer to the last one is “when it’s horny”.

Further Discussion

Attachments

• Slides